Annihilation cross section

Calculate the annihilation cross section, \(\langle \sigma v \rangle\) for the various annihilation channels of the model.

import matplotlib.pyplot as plt
import numpy as np
from singletscalar_dm import *

In order to calculate the annihilation cross section you can use the function: sigmav_channels. The example below calculates the annihilation cross section for the channel ‘bb’.

mS = 70 # GeV
lambda_hs = 0.01
sigmav_bb = sigmav_channels(mS,lambda_hs,'bb')
print(sigmav_bb)

1.346728994901666e-28

The possible choices for the channels are: ‘cc’, ‘bb’, ‘tt’, ‘tautau’, ‘gg’, ‘ww’, ‘zz’, ‘hh’, ‘aa’, ‘za’. It is possible to specify ‘tot’ to take into account all the previous channels together.

mS = 200 # GeV
lambda_hs = 0.01
sigmav_tot = sigmav_channels(mS,lambda_hs,'tot')
print(sigmav_tot)

4.680000000006868e-28

This is equivalent to summing all the different channels together.

mS = 200 # GeV
lambda_hs = 0.01
sigmav_tot = 0
channels_vec = np.array(['cc','bb','tt','tautau','gg','ww','zz','hh','aa','za'])
for t in range(len(channels_vec)):
    sigmav_tot += sigmav_channels(mS,lambda_hs,channels_vec[t])
print(sigmav_tot)

4.668283600003697e-28

It is possible to calculate the relative contribution of the different channels to the total cross section.

Br_cc = np.zeros(len(massz_vec))
Br_bb = np.zeros(len(massz_vec))
Br_tt = np.zeros(len(massz_vec))
Br_tautau = np.zeros(len(massz_vec))
Br_gg = np.zeros(len(massz_vec))
Br_ww = np.zeros(len(massz_vec))
Br_zz = np.zeros(len(massz_vec))
Br_hh = np.zeros(len(massz_vec))
Br_aa = np.zeros(len(massz_vec))
Br_za = np.zeros(len(massz_vec))
for t in range(len(massz_vec)):
    total_contribution = sigmav_channels(massz_vec[t],0.001,'tot')
    Br_cc[t] = sigmav_channels(massz_vec[t],0.001,'cc')/total_contribution
    Br_bb[t] = sigmav_channels(massz_vec[t],0.001,'bb')/total_contribution
    Br_tt[t] = sigmav_channels(massz_vec[t],0.001,'tt')/total_contribution
    Br_tautau[t] = sigmav_channels(massz_vec[t],0.001,'tautau')/total_contribution
    Br_gg[t] = sigmav_channels(massz_vec[t],0.001,'gg')/total_contribution
    Br_ww[t] = sigmav_channels(massz_vec[t],0.001,'ww')/total_contribution
    Br_zz[t] = sigmav_channels(massz_vec[t],0.001,'zz')/total_contribution
    Br_hh[t] = sigmav_channels(massz_vec[t],0.001,'hh')/total_contribution
    Br_aa[t] = sigmav_channels(massz_vec[t],0.001,'aa')/total_contribution
    Br_za[t] = sigmav_channels(massz_vec[t],0.001,'za')/total_contribution

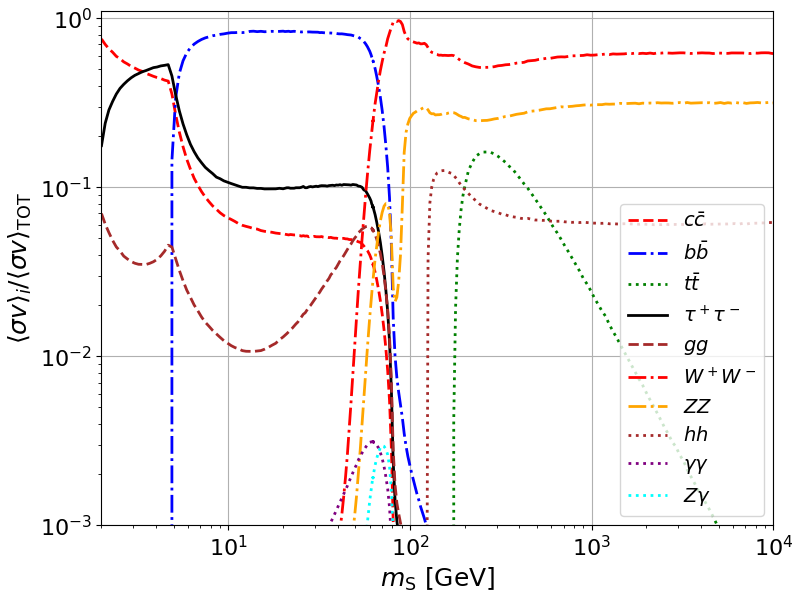
Which we can further plot.

fig = plt.figure(figsize=(8,6))
plt.plot(massz_vec,Br_cc, color='red', ls='--', lw=2.0, label=r'$c\bar{c}$' )
plt.plot(massz_vec,Br_bb, color='blue', ls='-.', lw=2.0, label=r'$b\bar{b}$' )
plt.plot(massz_vec,Br_tt, color='green', ls=':', lw=2.0, label=r'$t\bar{t}$' )
plt.plot(massz_vec,Br_tautau, color='black', ls='-', lw=2.0, label=r'$\tau^+\tau^-$' )
plt.plot(massz_vec,Br_gg, color='brown', ls='--', lw=2.0, label=r'$gg$' )
plt.plot(massz_vec,Br_ww, color='red', ls='-.', lw=2.0, label=r'$W^+W^-$' )
plt.plot(massz_vec,Br_zz, color='orange', ls='-.', lw=2.0, label=r'$ZZ$' )
plt.plot(massz_vec,Br_hh, color='brown', ls=':', lw=2.0, label=r'$hh$' )
plt.plot(massz_vec,Br_aa, color='purple', ls=':', lw=2.0, label=r'$\gamma\gamma$' )
plt.plot(massz_vec,Br_za, color='cyan', ls=':', lw=2.0, label=r'$Z\gamma$' )
plt.ylabel(r'$\langle \sigma v \rangle_i/\langle \sigma v \rangle_{\rm{TOT}}$', fontsize=18)
plt.xlabel(r'$m_{\rm{S}}$ [GeV]', fontsize=18)
plt.axis([2,1e4,1e-3,1.1])
plt.xticks(fontsize=16)
plt.yticks(fontsize=16)
plt.grid(True)
plt.yscale('log')
plt.xscale('log')
plt.legend(loc=4,prop={'size':14},numpoints=1, scatterpoints=1, ncol=1)
fig.tight_layout(pad=0.5)
plt.show()

Furthermore, it is interesting to have a look at the thermal cross section. We import the data file.

table_int = np.loadtxt(import_data_file('SHP_sigmav_table.dat'))
sigmav_relic = np.zeros(len(massz_vec))
for t in range(len(massz_vec)):
    lambda_val =  interpolate_relicdensity(massz_vec[t],'QCDB')
    sigmav_relic[t] = lambda2sigmav(massz_vec[t],lambda_val,table_int)

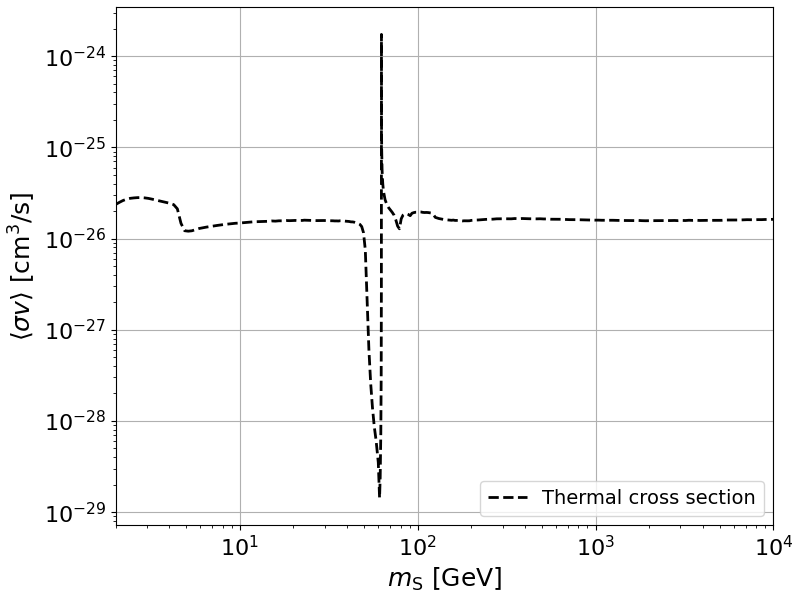
And we plot the \(\langle \sigma v \rangle\) as a function of \(m_S\).

fig = plt.figure(figsize=(8,6))
plt.plot(massz_vec,sigmav_relic, color='black', ls='--', lw=2.0, label=r'Thermal cross section' )
plt.ylabel(r'$\langle \sigma v \rangle$ [cm$^3$/s]', fontsize=18)
plt.xlabel(r'$m_{\rm{S}}$ [GeV]', fontsize=18)
plt.axis([2,1e4,0.5*sigmav_relic.min(),2*sigmav_relic.max()])
plt.xticks(fontsize=16)
plt.yticks(fontsize=16)
plt.grid(True)
plt.yscale('log')
plt.xscale('log')
plt.legend(loc=4,prop={'size':14},numpoints=1, scatterpoints=1, ncol=1)
fig.tight_layout(pad=0.5)
plt.show()