Relic density calculations

Calculate the relic density of the model.

import matplotlib.pyplot as plt
import numpy as np
from singletscalar_dm import *

In order to calculate the relic density it is possible to use the function interpolate_Omega, which uses the code DRAKE near the Higgs resonance and MicrOMEGAs elsewhere. For example, let’s compute the relic density, expressed as \(\Omega h^2\) for the QCDA model.

mS = 50 # GeV
lambda_hs = 0.1
omegah2 = interpolate_Omega(mS,lambda_hs,'QCDA',True)
print(omegah2)

0.12801745167589393

In the following, we compute the relic density using only MicrOMEGAs.

mS = 50 # GeV
lambda_hs = 0.1
omegah2_micromegas = interpolate_Omega_MicrOMEGAs(mS,lambda_hs)
print(omegah2_micromegas)

0.12796691577839414

As expected the results obtained with the functions interpolate_Omega and interpolate_Omega_MicrOMEGAs are similar for the mass point tested above. However, if we test masses close to the Higgs resonance the differences emerge:

mS = 60 # GeV
lambda_hs = 0.001
omegah2 = interpolate_Omega(mS,lambda_hs,'QCDA',True)
omegah2_micromegas = interpolate_Omega_MicrOMEGAs(mS,lambda_hs)
print(omegah2)
print(omegah2_micromegas)

0.06396689881423608
0.047495662241396217

The calculation of the relic density close to the resonance with DRAKE has been done for lambda_hs values between 1 and two orders of magnitude below and above the value that gives the correct relic abundance. If one tries to calculate the relic density with DRAKE beyond this region a warning will be printed.

mS = 60 # GeV
lambda_hs = 0.1
omegah2 = interpolate_Omega(mS,lambda_hs,'QCDA',True)
print(omegah2)

Warning, extrapolating.....
The relic density with DRAKE has been calculated for lambda_HS between  7.32e-05 0.01464
Following Value of lambda_HS is given 0.1
46.92619215842866

Note that the precomputed results with DRAKE have been done to cover the region which gives the right relic abundance, so investigating region beyond the tested one is not recommended. It is also possible to find the \(\lambda_{HS}\) value which provides a give relic density. In order to do that you can use the function interpolate_lambda

mS = 60 # GeV
Omegah2 = 0.1
lambda_hs = interpolate_lambda(mS,Omegah2,'QCDB',True)
print(lambda_hs)

0.0013339697597695931

Note that for dark matter masses below 70 GeV and \(\lambda_{HS}\) values larger than 1 the relic density have a turning point. See the following plot.

mass = 45
lambda_vec = np.logspace(-4.,2.,50)
omegah2_vec = np.zeros(len(lambda_vec))
for t in range(len(lambda_vec)):
    omegah2_vec[t] = interpolate_Omega_MicrOMEGAs(mass,lambda_vec[t])

fig = plt.figure(figsize=(8,6))
plt.plot(lambda_vec,omegah2_vec,lw=1.5,ls='-',color='black',label='$m_S=45$ GeV')
plt.ylabel(r'$\Omega h^2$', fontsize=18)
plt.xlabel(r'$\lambda_{HS}$', fontsize=18)
plt.axis([1e-4,100,1e-4,1e2])
plt.xticks(fontsize=16)
plt.yticks(fontsize=16)
plt.grid(True)
plt.yscale('log')
plt.xscale('log')
plt.legend(loc=4,prop={'size':14},numpoints=1, scatterpoints=1, ncol=1)
fig.tight_layout(pad=0.5)
plt.show()

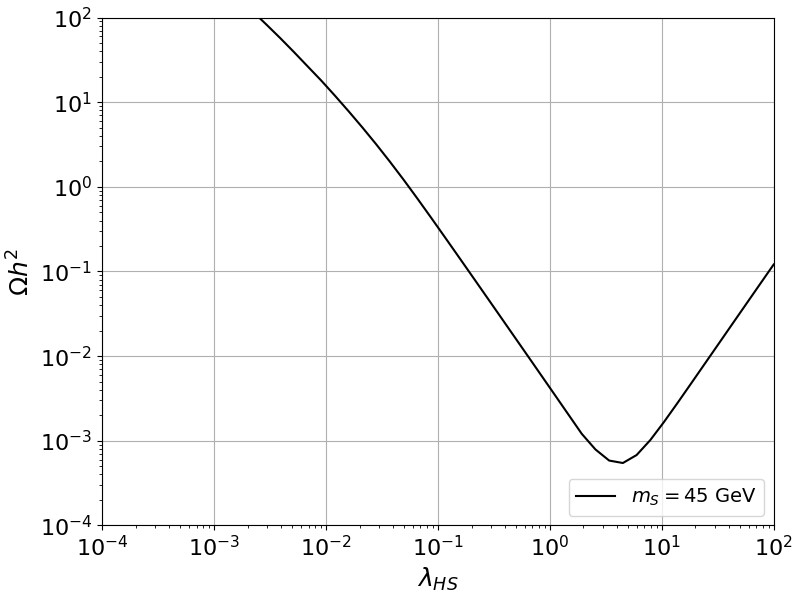
This implies that for \(m_S < 70\) GeV there could be two possible for the \(\lambda_{HS}\) which gives a value of the relic density. The code prints a warning if this is the case. See example below.

mS = 30 # GeV
Omegah2 = 0.001
lambda_hs = interpolate_lambda(mS,Omegah2,'QCDB',True)
print(lambda_hs)

Warning, extrapolating.
For this mass pick a range of Omegah^2 between  0.001075 984200.0
Following Value of Omegah^2 is given  0.001
0

mS = 70 # GeV
lambda_hs = 0.80952387
lambda_hs = interpolate_Omega(mS,lambda_hs,'QCDA',True)
print(lambda_hs)

0.0009975472734606318

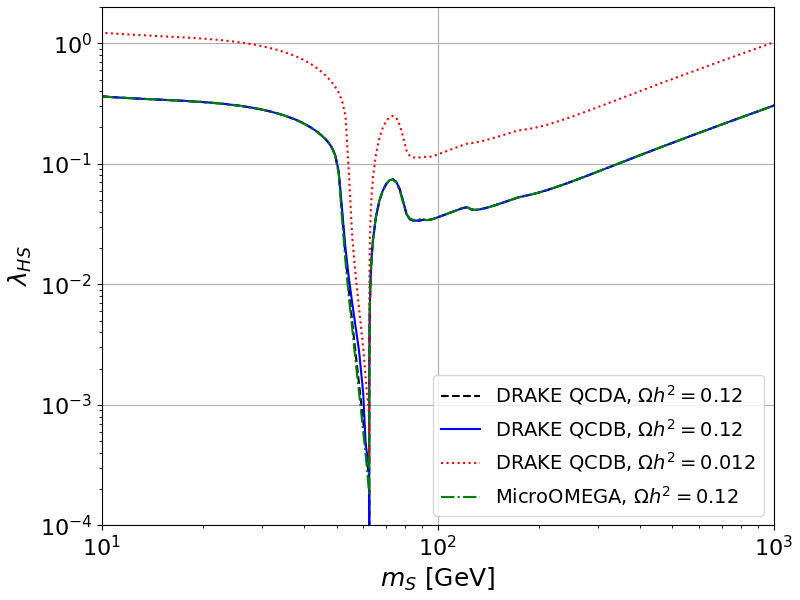
In the following, we will generate a plot with the values of \(m_S\) and \(\lambda_{HS}\) which provide 100% or 30% of the relic density, showing the calculations performed with the QCDA and QCDB models and with MicrOMEGAs.

mass_vec = massz_vec
lambda_QCDA_100_vec = np.zeros(len(mass_vec))
lambda_QCDB_100_vec = np.zeros(len(mass_vec))
lambda_QCDB_30_vec = np.zeros(len(mass_vec))
lambda_Micro_100_vec = np.zeros(len(mass_vec))
Omegah2 = 0.120
for t in range(len(mass_vec)):
    lambda_QCDA_100_vec[t] = interpolate_lambda(mass_vec[t],Omegah2,'QCDA',False)
    lambda_QCDB_100_vec[t] = interpolate_lambda(mass_vec[t],Omegah2,'QCDB',False)
    lambda_QCDB_30_vec[t] = interpolate_lambda(mass_vec[t],0.1*Omegah2,'QCDB',False)
    lambda_Micro_100_vec[t] = interpolate_lambda_MicrOMEGAs(mass_vec[t],Omegah2,False)

Warning, mass should be between 2.0 20000.0
Following Value of mass is given 2.0
Warning, mass should be between 2.0 20000.0
Following Value of mass is given 2.0
Warning, mass should be between 2.0 20000.0
Following Value of mass is given 2.0
Warning, mass should be between 2.0 20000.0
Following Value of mass is given 2.0

fig = plt.figure(figsize=(8,6))
plt.plot(mass_vec,lambda_QCDA_100_vec,lw=1.5,ls='--',color='black',label='DRAKE QCDA, $\Omega h^2=0.12$')
plt.plot(mass_vec,lambda_QCDB_100_vec,lw=1.5,ls='-',color='blue',label='DRAKE QCDB, $\Omega h^2=0.12$')
plt.plot(mass_vec,lambda_QCDB_30_vec,lw=1.5,ls=':',color='red',label='DRAKE QCDB, $\Omega h^2=0.012$')
plt.plot(mass_vec,lambda_Micro_100_vec,lw=1.5,ls='-.',color='green', label=r'MicroOMEGA, $\Omega h^2=0.12$')
plt.ylabel(r'$\lambda_{HS}$', fontsize=18)
plt.xlabel(r'$m_{S}$ [GeV]', fontsize=18)
plt.axis([10.,1000,1e-4,2e0])
plt.xticks(fontsize=16)
plt.yticks(fontsize=16)
plt.grid(True)
plt.yscale('log')
plt.xscale('log')
plt.legend(loc=4,prop={'size':14},numpoints=1, scatterpoints=1, ncol=1)
fig.tight_layout(pad=0.5)
plt.show()

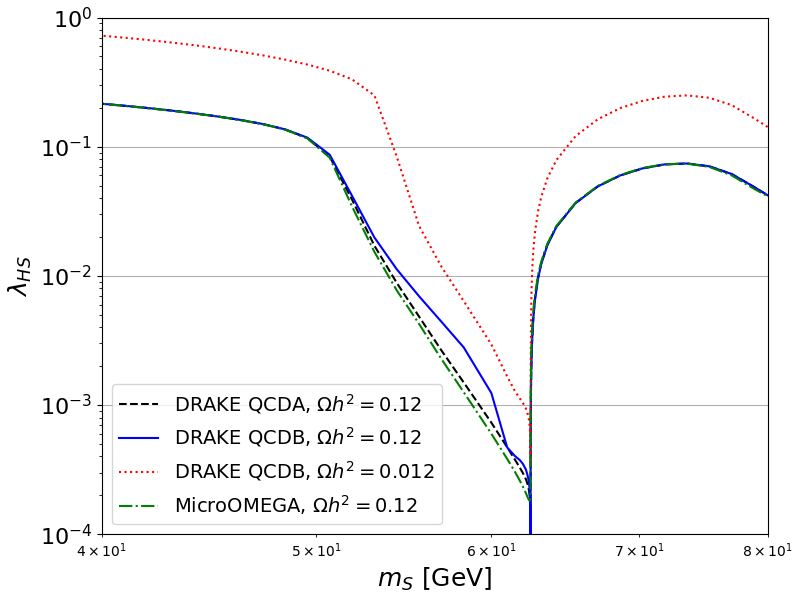
fig = plt.figure(figsize=(8,6))
plt.plot(mass_vec,lambda_QCDA_100_vec,lw=1.5,ls='--',color='black',label='DRAKE QCDA, $\Omega h^2=0.12$')
plt.plot(mass_vec,lambda_QCDB_100_vec,lw=1.5,ls='-',color='blue',label='DRAKE QCDB, $\Omega h^2=0.12$')
plt.plot(mass_vec,lambda_QCDB_30_vec,lw=1.5,ls=':',color='red',label='DRAKE QCDB, $\Omega h^2=0.012$')
plt.plot(mass_vec,lambda_Micro_100_vec,lw=1.5,ls='-.',color='green', label=r'MicroOMEGA, $\Omega h^2=0.12$')
plt.ylabel(r'$\lambda_{HS}$', fontsize=18)
plt.xlabel(r'$m_{S}$ [GeV]', fontsize=18)
plt.axis([40.,80,1e-4,1e0])
plt.xticks(fontsize=16)
plt.yticks(fontsize=16)
plt.grid(True)
plt.yscale('log')
plt.xscale('log')
plt.legend(loc=3,prop={'size':14},numpoints=1, scatterpoints=1, ncol=1)
fig.tight_layout(pad=0.5)
plt.show()

• 
• 

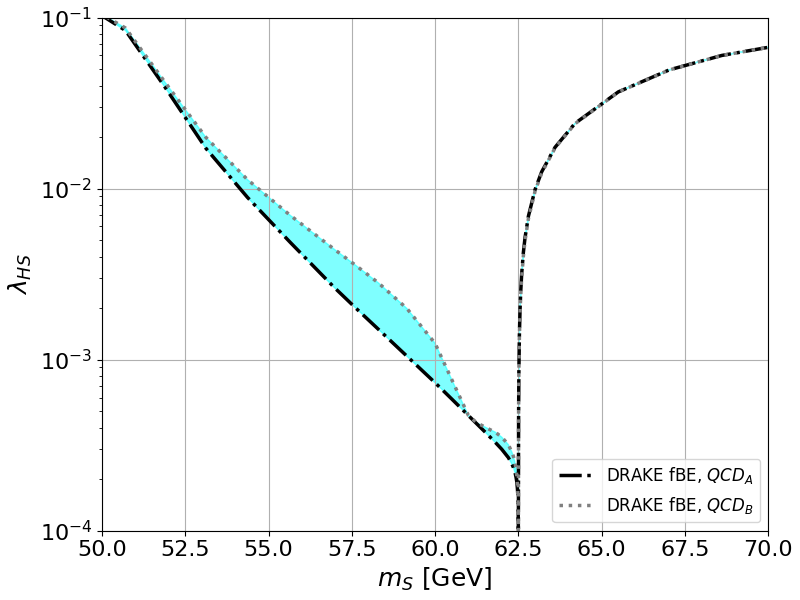
The parameters \(m_S\) and \(\lambda_{HS}\) which provide the right relic abundance are reported in the file Omega_MicroOMEGAs_DRAKE_QCDB_QCDA.dat, which can be imported through the function import_data_file.

omega_drake_micromegas = import_data_file('Omega_MicroOMEGAs_DRAKE_QCDB_QCDA.dat')
table = np.loadtxt(omega_drake_micromegas)
mass_RD = table[:,0]
lambda_RD_FBQCDA = table[:,1]
lambda_RD_FBQCDB = table[:,2]
fig = plt.figure(figsize=(8,6))
plt.fill_between(mass_RD,lambda_RD_FBQCDA,lambda_RD_FBQCDB,color='cyan',alpha=0.5)
plt.plot(mass_RD,lambda_RD_FBQCDA,lw=2.5,ls='-.',color='black', label=r'DRAKE fBE, $QCD_A$')
plt.plot(mass_RD,lambda_RD_FBQCDB,lw=2.5,ls=':',color='grey', label=r'DRAKE fBE, $QCD_B$')
plt.ylabel(r'$\lambda_{HS}$', fontsize=18)
plt.xlabel(r'$m_{S}$ [GeV]', fontsize=18)
plt.axis([50.,70,1e-4,1e-1])
plt.xticks(fontsize=16)
plt.yticks(fontsize=16)
plt.grid(True)
plt.yscale('log')
plt.xscale('linear')
plt.legend(loc=4,prop={'size':12},numpoints=1, scatterpoints=1, ncol=1)
fig.tight_layout(pad=0.5)
plt.show()