Indirect detection

This example studies the likelihoods for different indirect detection searches.

import matplotlib.pyplot as plt
import numpy as np
from scipy.interpolate import interp2d
from singletscalar_dm import *

table_int = np.loadtxt(import_data_file('SHP_sigmav_table.dat'))

Here we define the vectors for the annihilation cross section, mass and lambda_hs

sigmav_vec = np.power(10.,np.arange(-29.,-20.96,0.04))
mass_vec = massz_vec[19:224]
lambdap_vec = np.power(10.,np.arange(-6.,0.,0.04))

Here we create the likelihood profile for dwarf.

table_dwarf = np.loadtxt(import_data_file('LogLike_stacked_paper_SHP.dat'))
LogLike_table_dwarf = np.zeros(shape=(len(sigmav_vec),len(mass_vec)))
for t in range(len(mass_vec)):
    for u in range(len(sigmav_vec)):
        LogLike_table_dwarf[u,t] = -2.*table_dwarf[t*len(sigmav_vec)+u,3]
funcint_dwarf = interp2d(mass_vec,sigmav_vec,LogLike_table_dwarf)

LogLikel_table_dwarf = np.zeros(shape=(len(lambdap_vec),len(mass_vec)))
for t in range(len(mass_vec)):
    for u in range(len(lambdap_vec)):
        sigmav_val = lambda2sigmav(mass_vec[t],lambdap_vec[u],table_int)
        LogLikel_table_dwarf[u,t] = funcint_dwarf(mass_vec[t],sigmav_val)

Here we create the likelihood profile for dwarf.

table_pbar = np.loadtxt(import_data_file('LogLike_Manconi2021_pbar_paper.dat'))
LogLike_table_pbar = np.zeros(shape=(len(sigmav_vec),len(mass_vec)))
for t in range(len(mass_vec)):
    for u in range(len(sigmav_vec)):
        LogLike_table_pbar[u,t] = table_pbar[t*len(sigmav_vec)+u,2]
funcint_pbar = interp2d(mass_vec,sigmav_vec,LogLike_table_pbar)

LogLikel_table_pbar = np.zeros(shape=(len(lambdap_vec),len(mass_vec)))
for t in range(len(mass_vec)):
    for u in range(len(lambdap_vec)):
        sigmav_val = lambda2sigmav(mass_vec[t],lambdap_vec[u],table_int)
        LogLikel_table_pbar[u,t] = funcint_pbar(mass_vec[t],sigmav_val)

Here we consider the \(\chi^2\) for the GCE, relative to the MED model.

table_gce = np.loadtxt(import_data_file('Chi_table_Cholis_GCE_MED_paper.dat'))
LogLike_table_gce = np.zeros(shape=(len(sigmav_vec),len(mass_vec)))
for t in range(len(mass_vec)):
    for u in range(len(sigmav_vec)):
        LogLike_table_gce[u,t] = -table_gce[t*len(sigmav_vec)+u,2]
funcint_gce = interp2d(mass_vec,sigmav_vec,LogLike_table_gce)

LogLikel_table_gce = np.zeros(shape=(len(lambdap_vec),len(mass_vec)))
for t in range(len(mass_vec)):
    for u in range(len(lambdap_vec)):
        sigmav_val = lambda2sigmav(mass_vec[t],lambdap_vec[u],table_int)
        LogLikel_table_gce[u,t] = funcint_gce(mass_vec[t],sigmav_val)

Further, we combine the likelihoods.

LogLike_table_combined = LogLike_table_gce+LogLike_table_pbar+LogLike_table_dwarf
LogLikel_table_combined = LogLikel_table_gce+LogLikel_table_pbar+LogLikel_table_dwarf

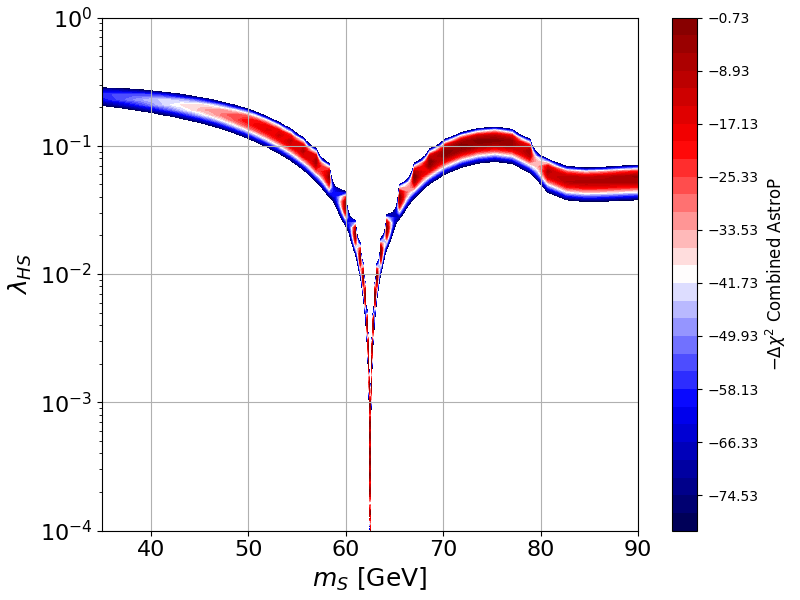
And we plot the results.

fig, ax = plt.subplots(figsize=(8,6))

dlin = ( 80+2 )/30.
scale_vec = np.arange( -80,2, dlin )
scale_cb = np.arange( -80,2, dlin*10.)

cf = ax.contourf(mass_vec, lambdap_vec, LogLikel_table_combined-LogLikel_table_combined.max(), 30, levels=list(scale_vec), cmap='seismic')
cbar = fig.colorbar(cf, ax = ax)
cbar.ax.set_ylabel(r'$-\Delta\chi^2$ Combined AstroP', fontsize="large")

plt.ylabel(r'$\lambda_{HS}$', fontsize=18)
plt.xlabel(r'$m_{S}$ [GeV]', fontsize=18)
plt.axis([35.,90,1e-4,1.0])
plt.xticks(fontsize=16)
plt.yticks(fontsize=16)
plt.grid(True)
plt.yscale('log')
plt.xscale('linear')
fig.tight_layout(pad=0.5)
plt.show()

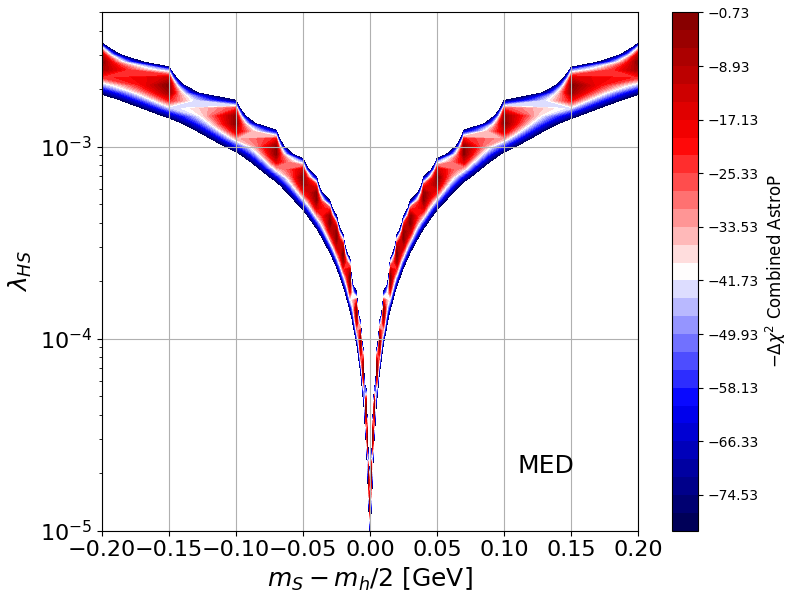
fig, ax = plt.subplots(figsize=(8,6))

dlin = ( 80+2 )/30.
scale_vec = np.arange( -80,2, dlin )
scale_cb = np.arange( -80,2, dlin*10.)

cf = ax.contourf(mass_vec-62.50, lambdap_vec, LogLikel_table_combined-LogLikel_table_combined.max(), 30, levels=list(scale_vec), cmap='seismic')
cbar = fig.colorbar(cf, ax = ax)
cbar.ax.set_ylabel(r'$-\Delta\chi^2$ Combined AstroP', fontsize="large")

plt.text(0.11,2e-5,'MED', fontsize=18)
plt.ylabel(r'$\lambda_{HS}$', fontsize=18)
plt.xlabel(r'$m_{S}-m_h/2$ [GeV]', fontsize=18)
plt.axis([-0.2,0.2,1e-5,0.005])
plt.xticks(fontsize=16)
plt.yticks(fontsize=16)
plt.grid(True)
plt.yscale('log')
plt.xscale('linear')
fig.tight_layout(pad=0.5)
plt.show()

Here we create the likelihood profile for antiprotons from Balan et al. 2023.

table_pbar = np.loadtxt(import_data_file('LogLike_sigmav_Manconi2023_model1_corr_pbar_paper.dat'))
LogLike_table_pbar = np.zeros(shape=(len(sigmav_vec),len(mass_vec)))
for t in range(len(mass_vec)):
    for u in range(len(sigmav_vec)):
        LogLike_table_pbar[u,t] = table_pbar[t*len(sigmav_vec)+u,2]
funcint_pbar = interp2d(mass_vec,sigmav_vec,LogLike_table_pbar)

LogLikel_table_pbar = np.zeros(shape=(len(lambdap_vec),len(mass_vec)))
for t in range(len(mass_vec)):
    for u in range(len(lambdap_vec)):
        sigmav_val = lambda2sigmav(mass_vec[t],lambdap_vec[u],table_int)
        LogLikel_table_pbar[u,t] = funcint_pbar(mass_vec[t],sigmav_val)

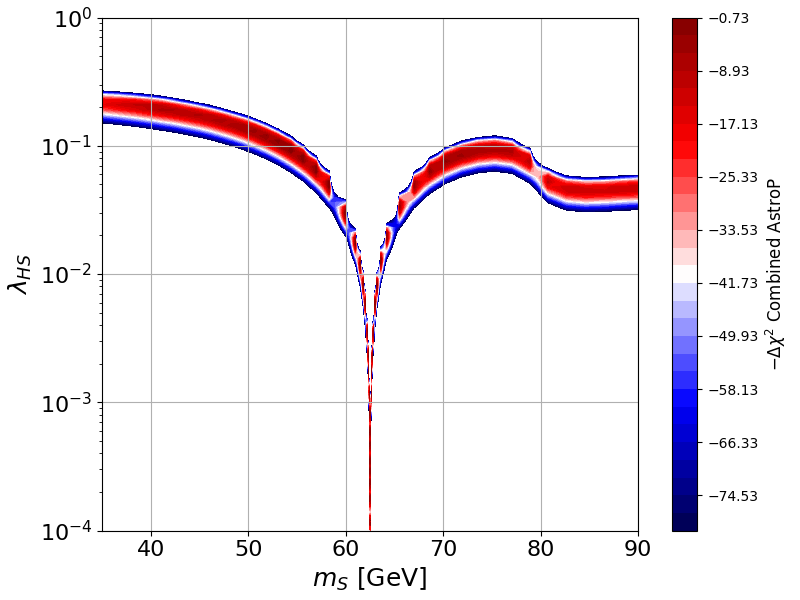
We then combine the likelihoods.

LogLike_table_combined = LogLike_table_gce+LogLike_table_pbar+LogLike_table_dwarf
LogLikel_table_combined = LogLikel_table_gce+LogLikel_table_pbar+LogLikel_table_dwarf

And we plot the results.

fig, ax = plt.subplots(figsize=(8,6))

dlin = ( 80+2 )/30.
scale_vec = np.arange( -80,2, dlin )
scale_cb = np.arange( -80,2, dlin*10.)

cf = ax.contourf(mass_vec, lambdap_vec, LogLikel_table_combined-LogLikel_table_combined.max(), 30, levels=list(scale_vec), cmap='seismic')
cbar = fig.colorbar(cf, ax = ax)
cbar.ax.set_ylabel(r'$-\Delta\chi^2$ Combined AstroP', fontsize="large")

plt.ylabel(r'$\lambda_{HS}$', fontsize=18)
plt.xlabel(r'$m_{S}$ [GeV]', fontsize=18)
plt.axis([35.,90,1e-4,1.0])
plt.xticks(fontsize=16)
plt.yticks(fontsize=16)
plt.grid(True)
plt.yscale('log')
plt.xscale('linear')
fig.tight_layout(pad=0.5)
plt.show()